Abstract
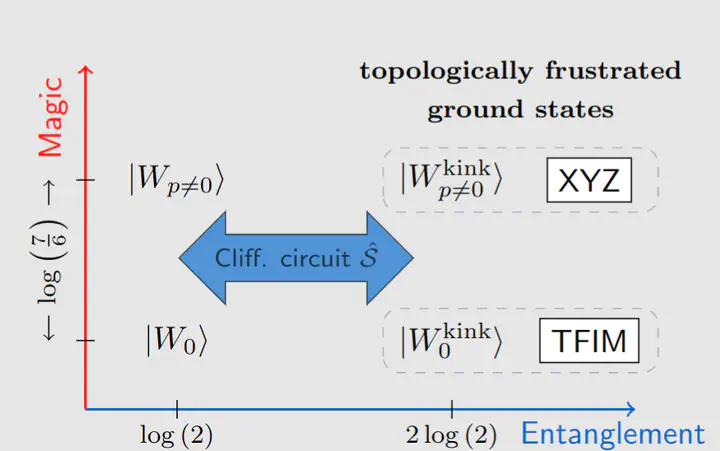
We employ the Stabilizer Renyi Entropy (SRE) to characterize a quantum phase transition that has so far eluded any standard description and can thus now be explained in terms of the interplay between its non-stabilizer properties and entanglement. The transition under consideration separates a region with a unique ground state from one with a degenerate ground state manifold spanned by states with finite and opposite (intensive) momenta. We show that SRE has a jump at the crossing points, while the entanglement entropy remains continuous. Moreover, by leveraging on a Clifford circuit mapping, we connect the observed jump in SRE to that occurring between standard and generalized W-states with finite momenta. This mapping allows us to quantify the SRE discontinuity analytically.