Abstract
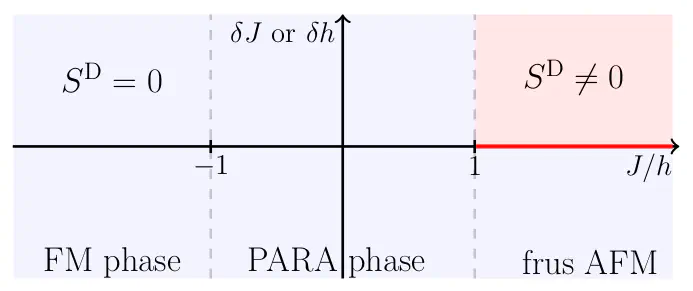
Topological order comes in different forms, and its classification and detection is an important field of modern research. In this work, we show that the Disconnected Entanglement Entropy, a measure originally introduced to identify topological phases, is also able to unveil the long-range entanglement (LRE) carried by a single, fractionalized excitation. We show this by considering a quantum, delocalized domain wall excitation that can be introduced into a system by inducing geometric frustration in an antiferromagnetic spin chain. Furthermore, we show that the LRE of such systems is resilient against a quantum quench and the introduction of disorder, as it happens in traditional symmetry-protected topological phases. All these evidences establish the existence of a new phase induced by frustration with topological features despite not being of the usual type.