Extensive Robustness of Entanglement in Quantum Spin Chains
Abstract
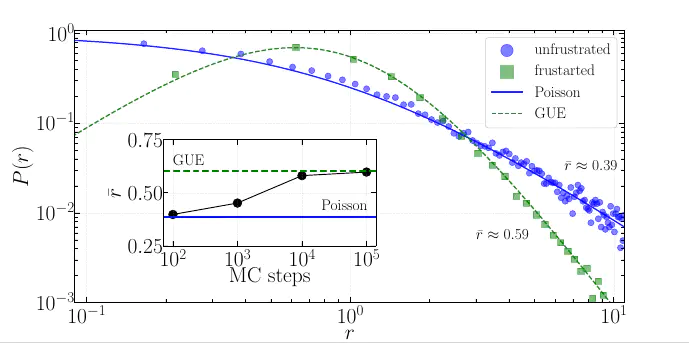
Entanglement is recognized as a primary resource for quantum advantage. We explore the resilience of various kinds of entanglement in the ground state of a local Hamiltonian against the application of random local unitaries, acting at most on two neighboring sites of a 1D spin chain. We distinguish two classes of operations, depending on whether they preserve or not the symmetries of the Hamiltonian. The latter are more efficient in destroying the entanglement, but also change its nature by making it more complex. Adding topological frustration to the chain adds additional, non-local entanglement, which cannot be completely destroyed by the local unitaries. Our work highlights a subtle interplay between locality and non-local constraint. Manuscript in preparation.